Recuadros para mapas en Geopandas
Cómo hacer distintos tipos de recuadros para mapas hechos con Geopandas
- Introducción
- Datos
- Recuadro de acercamiento
- Recuadro de contexto
- Escalas
- Recuadro de áreas no contiguas
- Revisa otras entradas de este blog:
Introducción
Con la reciente publicación de los resultados del censo 2020 de INEGI varios usuarios han estado presentando algunas gráficas en redes sociales con los principales resultados. Una de las visualizaciones más populares son los mapas coropléticos, especialmente a nivel municipal. Una ventaja de estos mapas es que nos permiten tener el panorama general de todo el país e incluso detectar a grandes rasgos algunos patrones regionales. Por ejemplo, acá @claudiodanielpc nos muestra el hacinamiento en los hogares:
Siguiendo con los microdatos del #Censo2020Mx, hice este mapa en #rstats sobre el hacinamiento en cada municipio.
— Claudio Daniel Pacheco-Castro (@claudiodanielpc) March 22, 2021
Gracias al Dr. @SantaellaJulio y al gran equipo del @INEGI_INFORMA por brindarnos información para el análisis de los problemas de nuestro país. pic.twitter.com/K9zhJkSmEt
Sin embargo, un inconveniente es que hay casos de regiones donde hay un gran número de municipios en una superficie pequeña lo que dificulta la lectura de la información. Un caso común en México es el área compuesta por los estados de Oaxaca, Puebla, Chiapas, Veracruz y Estado de México que contienen 1248 municipios, poco más de la mitad del total de 2469 municipios. Muchos mapas se vuelven difícil de ver en esta zona. Por ejemplo:
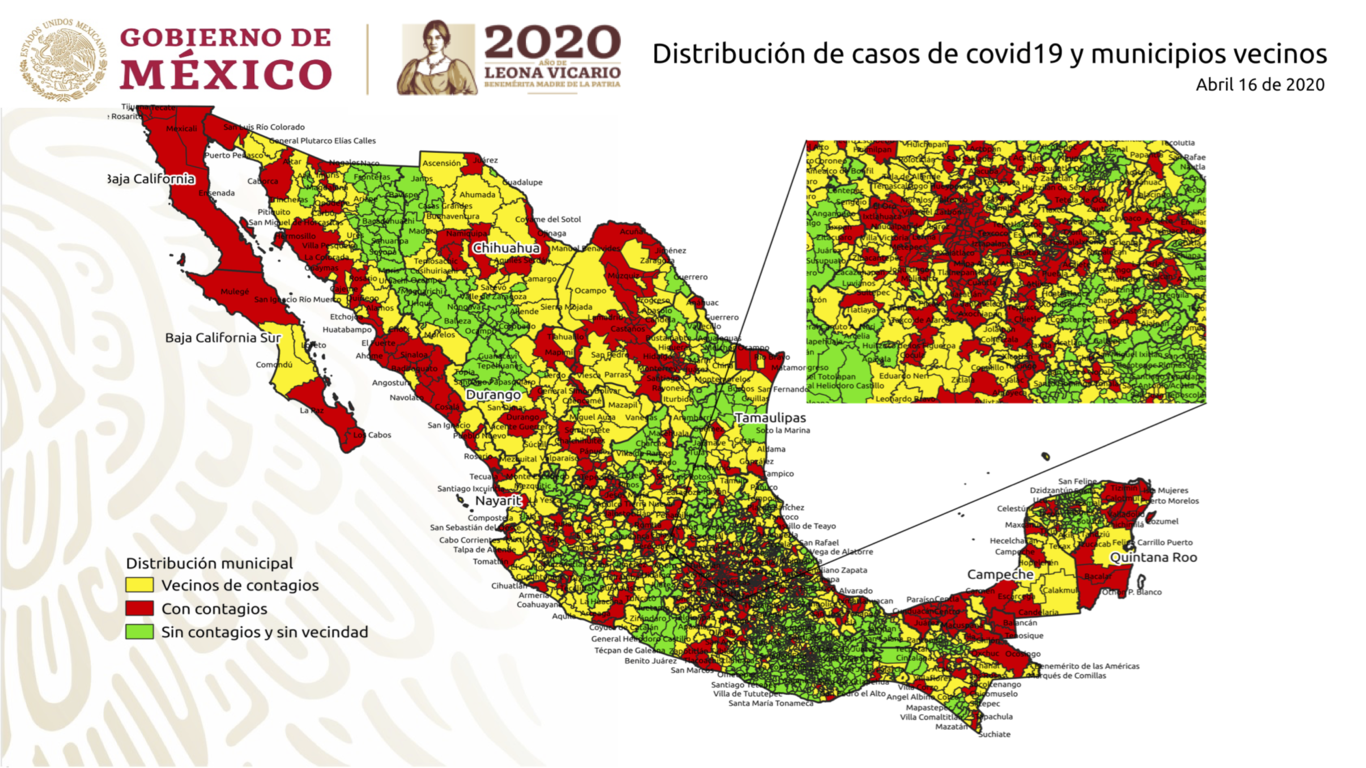
Para tratar de hacer más claras este tipo de visualizaciones podemos agregar uno o varios recuadros con acercamiento (zoom) a los resultados de estas zonas, tal como lo hace el mapa del ejemplo. Si bien eso no garantiza que toda la información se entenderá mejor, al menos puede ayudar en ciertas áreas. En esta entrada veremos cómo hacer varios tipos de recuadros para mapas en Python usando Geopandas y Matplotlib.
Empecemos importando las librerías necesarias.
import os
import sys
import geopandas as gpd
import matplotlib.pyplot as plt
import pandas as pd
import requests
import matplotlib_scalebar
from matplotlib_scalebar.scalebar import ScaleBar
print('Python', sys.version)
print(pd.__name__, pd.__version__)
print(gpd.__name__, gpd.__version__)
print(requests.__name__, requests.__version__)
print(plt.matplotlib.__name__, plt.matplotlib.__version__)
print(matplotlib_scalebar.__name__, matplotlib_scalebar.__version__)
Datos
Voy a usar una versión del mapa de México algo simplificada que pesa relativamente poco. Este shapefile puede descargarse aquí.
Leemos el archivo, asignamos la clave municipal de INEGI como el índice del GeoDataFrame y además reproyectamos las coordenadas usando el sistema de coordenadas Mexico ITRF92 / UTM zone 12N
mx = gpd.read_file('mapa_mexico/')\
.set_index('CLAVE')\
.to_crs(epsg=4485)
mx.head()
Al GeoDataFrame anterior vamos a añadirle datos para que podamos graficar un mapa coroplético. Usaremos la API de DataMéxico para obtener los datos del Índice de Complejidad Económica (ECI). La propia definición del ECI de DataMexico es:
El Índice de Complejidad Económica (ECI) mide las capacidades productivas de una localidad (e.g. estado o municipalidad) a partir de la presencia de actividades (e.g. empleo, industrias o exportaciones) en esa y otras localidades. La complejidad económica de una localidad predice su nivel de ingreso, crecimiento económico, desigualdad, y emisiones de gases de efecto invernadero.
En general, un ECI más alto indica un mayor nivel de sofisticación en los productos que se producen en un municipio. Así se ven los datos:
url = 'https://api.datamexico.org/tesseract/cubes/complexity_eci/aggregate.jsonrecords?cuts%5B%5D=Latest.Latest.Latest.1&drilldowns%5B%5D=Geography+Municipality.Geography.Municipality&drilldowns%5B%5D=Date+Day.Date.Year&measures%5B%5D=ECI&parents=false&sparse=false'
data_eci = requests.get(url).json()
eci = pd.DataFrame(data_eci['data'])\
.assign(CLAVE=lambda x: x['Municipality ID'].astype(str).str.zfill(5))\
.set_index('CLAVE')
eci.head()
El índice está estandarizado con una media de 0 y varianza de 1 y tiene un rango entre -1.4 y 4.9.
eci['ECI'].describe()
Revisamos su distribución:
eci['ECI'].hist(bins=100)
Ahora anexamos los datos del ECI al GeoDataFrame:
mx = mx.join(eci, how='left')
mx.head()
Creamos un par de GeoDataFrames que nos servirán más adelante:
-
oaxcontiene los datos solo para el estado de Oaxaca -
edoses un GeoDataFrame con los polígonos de los estados del país.
oax = mx.query('CVE_EDO=="20"')
edos = mx.dissolve(by='CVE_EDO')
Y ahora visualicemos el ECI con un esquema de cortes por quintiles:
fig, ax = plt.subplots()
mx.plot(column='ECI', legend=True, scheme='quantiles', k=5, cmap='viridis_r', ax=ax)
fig.set_size_inches(12, 8)
Como se puede ver, algunas zonas del centro y sur del país son difíciles de distinguir por el gran número de municipios que hay.
Recuadro de acercamiento
Vamos a añadir un recuadro de acercamiento o detalle a la zona sur, señalando principalmente los municipios del estado de Oaxaca. Para eso usaremos la función inset_axes de Matplotlib. Esta función nos permite añadir un nuevo objeto axes a nuestra gráfica en cualquier parte del gráfico. La función recibe una lista con 4 valores que son: $[x, y, w, h]$:
- $x$: posición en el eje x de la esquina inferior izquierda del recuadro
- $y$: posición en el eje y de la esquina inferior izquierda del recuadro
- $w$: ancho del recuadro
- $h$: altura del recuadro
Todos estos valores vienen expresados como proporción del tamaño de la gráfica (proporción del ancho para el eje x, proporción del alto para el eje y). Veamos un ejemplo:
fig, ax = plt.subplots()
axins = ax.inset_axes([1.1, 0.5, 0.4, 0.4])
axins.set(xlim=(0.5, 0.7), ylim=(0.4, 0.6))
ax.indicate_inset_zoom(axins)
Lo que hicimos fue añadir una figura (fig) y un objeto axes principal (ax). Luego añadimos el recuadro axins y limitamos el rango del eje $x$ e $y$ en los que se enfoca el recuadro. Por último, le indicamos al recuadro cuál es la gráfica principal sobre la que esta haciendo el zoom. Lo que falta es dibujar sobre los objetos ax y axins.
x = [0, 0.5, 0.6, 0.8]
y = [0, 0.4, 0.5, 0.3]
ax.plot(x, y, color='C0')
axins.plot(x, y, color='C0')
fig
Aunque es relativamente fácil añadir un recuadro a una gráfica, es un poco más difícil añadir el recuadro a un mapa. La dificultad adicional está en que en el resultado final los parámetros $x$, $y$, $w$ y $h$ no se comportan exactamente como sería esperado, sino que por algún motivo el recuadro queda en una posición un poco diferente. No podría asegurarlo, pero me parece que esto pasa porque al graficar un mapa Matplotlib modifica el tamaño de la gráfica y su relación de aspecto para ajustarlo a la información geográfica. La solución (muy poco satisfactoria) es jugar con varios valores de $x$, $y$, $w$ y $h$ hasta que la posición sea la adecuada.
En el siguiente ejemplo vamos a acercarnos al estado de Oaxaca con un recuadro usando los parámetros $x=0.82, y=0.05, w=0.9, h=0.9$ y poniendo como límite al eje x el rango (1820000, 2350000) y al eje y el rango (1780000, 2150000). Los valores (y su unidad de medida) de los ejes X e Y vienen dadas por el sistema de coordenadas geográficas que usamos.
fig, ax = plt.subplots()
# Añade recuadro
axins = ax.inset_axes([0.82, 0.05, 0.9, 0.9])
# Gráfica principal
mx.plot(column='ECI', legend=True, ax=ax, scheme='quantiles', k=5, cmap='viridis_r', legend_kwds={'loc': 'lower left'})
mx.boundary.plot(lw=0.05, color='k', ax=ax)
# Gráfica recuadro
mx.plot(column='ECI', legend=False, ax=axins, scheme='quantiles', k=5, cmap='viridis_r')
mx.boundary.plot(lw=0.25, color='k', ax=axins)
edos.boundary.plot(lw=1, color='red', ax=axins)
# limita área a mostrar
axins.set(ylabel='', xlabel='', xlim=(1820000, 2350000), ylim=(1780000, 2150000), xticks=[], yticks=[])
# Establece líneas del recuadro a la gráfica principal
ax.indicate_inset_zoom(axins)
# Tamaño de la gráfica final
fig.set_size_inches(12, 8)
El acercamiento resulta bastante bueno, ahora es posible identificar mejor los valores del ECI para el estado de Oaxaca y otros vecinos. Podemos añadir un segundo recuadro para ver los municipios del industrial estado de Guanajuato. El proceso es el mismo que el anterior, aunque ahora demorará más porque debe graficar más elementos.
fig, ax = plt.subplots()
# Añade recuadro 1
axins = ax.inset_axes([0.86, 0.05, 0.9, 0.9])
# Añade recuadro 2
axins2 = ax.inset_axes([0.2, -0.5, 0.5, 0.5])
# Gráfica principal
mx.plot(column='ECI', legend=True, ax=ax, scheme='quantiles', k=5, cmap='viridis_r', legend_kwds={'loc': 'lower left'})
mx.boundary.plot(lw=0.05, color='k', ax=ax)
# Gráfica recuadro 1
mx.plot(column='ECI', legend=False, ax=axins, scheme='quantiles', k=5, cmap='viridis_r')
mx.boundary.plot(lw=0.25, color='k', ax=axins)
edos.boundary.plot(lw=1, color='red', ax=axins)
# Gráfica recuadro 2
mx.plot(column='ECI', legend=False, ax=axins2, scheme='quantiles', k=5, cmap='viridis_r')
mx.boundary.plot(lw=0.25, color='k', ax=axins2)
edos.boundary.plot(lw=1, color='red', ax=axins2)
# limita área a mostrar recuadro 1 y 2
axins.set(ylabel='', xlabel='', xlim=(1820000, 2350000), ylim=(1780000, 2150000), xticks=[], yticks=[], title='Oaxaca')
axins2.set(ylabel='', xlabel='', xlim=(1425000, 1680000), ylim=(2229203, 2453767), xticks=[], yticks=[], title='Guanajuato')
# Elimina marco de la gráfica principal
ax.set_axis_off()
# Establece líneas de los recuadros a la gráfica principal
ax.indicate_inset_zoom(axins)
ax.indicate_inset_zoom(axins2)
# Tamaño de la gráfica final
fig.set_size_inches(12, 8)
Es notable la diferencia en la complejidad entre los municipios de Guanajuato y Oaxaca.
El pequeño recuadro al interior que señala el área del mapa principal que se está señalando no se nota mucho porque se confunde con el color de los polígonos. Para evitar eso, podemos recolorear el borde de los recuadros para que sea posible asociarlos usando el color. Esta idea la vi en un mapa creado por @ElenoAM 🤯 y me pareció incluso más limpia que tener varias líneas indicando el zoom.
Mapa del fracaso de la política de suelo y de vivienda de @FelipeCalderon y de @VicenteFoxQue.
— Adrián (@ElenoAM) March 11, 2021
Desarrollos inmobiliarios periurbanos, mal ubicados, sin servicios, empleo... pic.twitter.com/dvqZRi8euR
Veamos ahora cómo queda tras quitar las líneas y ponerle colores al borde de los recuadros.
fig, ax = plt.subplots()
# Añade recuadro 1
axins = ax.inset_axes([0.86, 0.05, 0.9, 0.9])
# Añade recuadro 2
axins2 = ax.inset_axes([0.2, -0.5, 0.5, 0.5])
# Gráfica principal
mx.plot(column='ECI', legend=True, ax=ax, scheme='quantiles', k=5, cmap='viridis_r', legend_kwds={'loc': 'lower left'})
mx.boundary.plot(lw=0.05, color='k', ax=ax)
# Gráfica recuadro 1
mx.plot(column='ECI', legend=False, ax=axins, scheme='quantiles', k=5, cmap='viridis_r')
mx.boundary.plot(lw=0.25, color='k', ax=axins)
edos.boundary.plot(lw=1, color='red', ax=axins)
# Gráfica recuadro 2
mx.plot(column='ECI', legend=False, ax=axins2, scheme='quantiles', k=5, cmap='viridis_r')
mx.boundary.plot(lw=0.25, color='k', ax=axins2)
edos.boundary.plot(lw=1, color='red', ax=axins2)
# limita área a mostrar recuadro 1 y 2
axins.set(ylabel='', xlabel='', xlim=(1820000, 2350000), ylim=(1780000, 2150000), xticks=[], yticks=[], title='Oaxaca')
axins2.set(ylabel='', xlabel='', xlim=(1425000, 1680000), ylim=(2229203, 2453767), xticks=[], yticks=[], title='Guanajuato')
# Elimina marco de la gráfica principal
ax.set_axis_off()
# Establece líneas de los recuadros a la gráfica principal
ax.indicate_inset_zoom(axins)
ax.indicate_inset_zoom(axins2)
# Parametros para cambiar colores
color_insets = ['red', 'blue']
color_index = 0
# colorea los cuadros interiores
for p in ax.patches:
if isinstance(p, plt.matplotlib.patches.Rectangle):
p.set_edgecolor(color_insets[color_index])
p.set_linewidth(2)
color_index += 1
else:
# Esconde las líneas hacia la gráfica principal
p.set_visible(False)
# Colorea el marco del recuadro 1 y aumenta grosor de línea
for sp in axins.spines.values():
sp.set_color(color_insets[0])
sp.set_linewidth(2)
# Colorea el marco del recuadro 2 y aumenta grosor de línea
for sp in axins2.spines.values():
sp.set_color(color_insets[1])
sp.set_linewidth(2)
# Tamaño final
fig.set_size_inches(12, 8)
Ahora es más fácil identificar el área que se está acercando.
Recuadro de contexto
En un recuadro de contexto el mapa principal corresponde a la región que vamos a analizar con detalle y usamos el recuadro para resaltar la posición de esa región con respecto al país. Para lograr este efecto no usamos la función ax.inset_axes(), sino una muy parecida que es fig.add_axes() y recibe los mismos argumentos $x, y, w, h$. La diferencia es que ahora no tendremos las líneas desde el recuadro hasta el mapa principal.
fig, ax = plt.subplots()
# Mapa principal
oax.plot(column='ECI', legend=True, scheme='quantiles', k=5, cmap='viridis_r', ax=ax)
# Borde de los municipios
oax.boundary.plot(linewidth=0.5, color='gray', ax=ax)
# Inserta recuadro
ax_mex = fig.add_axes([0.91, 0.11, 0.35, 0.35], )
# Dibuja los estados del país en el recuadro
edos.boundary.plot(color='gray', ax=ax_mex)
# Resalta Oaxaca con el color rojo
edos.query('CVE_EDO=="20"').plot(color='red', ax=ax_mex)
# Establece tamaño final
fig.set_size_inches(12, 8)
Escalas
Cuando graficamos mapas con distintos niveles de acercamiento/alejamiento es importante acompañar cada mapa con una barra de escala que nos permita saber cómo comparar longitudes. Para Matplotlib existe la excelente librería matplotlib-scalebar para agregar estas escalas y afortunadamente funciona bien con mapas de Geopandas. A continuación añadimos las escalas para cada mapa.
ax.set(xticks=[], yticks=[], title='Oaxaca')
ax_mex.set(xticks=[], yticks=[], title='México')
# Barras de escala
scalebar_oax = ScaleBar(1, "m", length_fraction=0.2, location='lower left', )
ax.add_artist(scalebar_oax)
scalebar_mex = ScaleBar(1, "m", length_fraction=0.25, location='lower left')
ax_mex.add_artist(scalebar_mex)
fig
De esta forma podemos reconocer mejor las dimensiones de Oaxaca y sus municipios con respecto a todo el país.
Recuadro de áreas no contiguas
Este tipo de recuadro sirve para mostrar juntas áreas que no están cerca o es muy difícil ver juntas en su ubicación normal. El primer caso que viene a mi cabeza es el del departamento de San Andrés y Providencia en Colombia 🟨🟨🟦🟥. San Andrés y Providencia son unas diminutas islas ubicadas a 774 km del noreste de Colombia y que conforman uno de los 32 departamentos del país. En los mapas de división política-administrativa del país estas islas siempre aparecen como recuadros al lado de la parte continental, con una escala mucho mayor para poder ser visibles.
Para visualizarlas usemos este mapa de Colombia con la división por departamentos que también puede descargarse desde el Marco Geostadístico Nacional. Usaremos el sistema de coordenadas MAGNA-SIRGAS / Colombia Bogota zone.
col = gpd.read_file('mapa_colombia/').to_crs(epsg=3116)
col.head()
Al graficar el mapa del país a duras penas podremos notar las islas en la parte superior derecha.
fig, ax = plt.subplots()
col.plot(ax=ax)
fig.set_size_inches(10, 10)
Para hacer un típico mapa político administrativo, vamos a añadir dos objetos axes con fig.add_axes() en los que graficaremos a cada isla. Para encontrar las coordenadas de las islas lo mejor es usar el mapa de http://epsg.io/map#srs=3116&x&y&z=10&layer=streets. También agregamos las barras de escala para dimensionar mejor lo pequeñas que son.
fig, ax = plt.subplots()
# Añade ax para San Andrés
ax_san = fig.add_axes([0.25, 0.75, 0.05, 0.1])
# Añade ax para Providencia
ax_prov = fig.add_axes([0.29, 0.77, 0.08, 0.08])
# Grafica Parte continental
col.plot(ax=ax)
# Grafica San Andrés
col.plot(ax=ax_san)
# Grafica Providencia
col.plot(ax=ax_prov)
# Limita los valores del eje x e y para cada gráfica
ax.set(ylim=(0, 1_900_000), xlim=(400_000, 1_850_000), yticks=[], xticks=[])
ax_san.set(ylim=(1_883_000, 1_902_000), xlim=(163_000, 172_000), yticks=[], xticks=[])
ax_prov.set(ylim=(1_975_000, 1_990_000), xlim=(204_044, 211_100), yticks=[], xticks=[])
# Títulos de las gráficas
ax.set_title('Colombia', fontsize=20)
ax_san.set_title('San\n Andrés', fontsize=7)
ax_prov.set_title('Providencia', fontsize=7)
# Añade barras de escala
scalebar_col = ScaleBar(1, "m", length_fraction=0.2, location='lower left', )
ax.add_artist(scalebar_col)
scalebar_san = ScaleBar(1, "m", length_fraction=1, location='upper center', font_properties={'size': 7})
ax_san.add_artist(scalebar_san)
scalebar_prov = ScaleBar(1, "m", length_fraction=0.8, location='upper center', box_alpha=0, font_properties={'size': 7})
ax_prov.add_artist(scalebar_prov)
# Tamaño final de la gráfica
fig.set_size_inches(10, 10)
Revisa otras entradas de este blog:
- Integración de PyQGIS con Jupyter Lab usando Anaconda
- Introducción a PyQGIS (Python + QGIS)
- Mapas de puntos con Python
- Introducción a bases de datos relacionales y SQL para científicos sociales
- Etiquetado de variables y valores en las encuestas de INEGI usando Python
- Generando archivos de Excel con formatos y gráficas usando Python
- Trabajando con archivos de Excel complejos en Pandas